论文题目: RobustNet: Improving Domain Generalization in Urban-Scene Segmentation via Instance Selective Whitening
作者: Sungha Choi, Sanghun Jung, Huiwon Yun, Joanne T. Kim, Seungryong Kim, Jaegul Choo
研究机构: LG AI Research, KAIST Korea University, Sogang University
摘要
本文提出了一种新颖的disentangle domain-specific style 和 domain-invariant content的方法,通过消除style信息带来的影响解决domain shift问题,无需增加额外的参数,并在三个unseen domain上取得了很好的分割的效果,总的来说是一种简单有效的方法,值得仔细研究。
研究背景
domain-generalization的现实意义
- 在自动驾驶领域,真实世界的数据是由意想不到的和看不见的样本组成的,例如,在不同光照、恶劣天气条件下或从不同地点拍摄的图像。一般来说,用有限的训练数据来建模这样一个完整的数据分布是不可能的,因此如何减小源域和目标域之间的域差一直是计算机视觉中一个长期存在的问题。
domain-generalization的现有工作存在问题
- DG问题可以通过利用instance normalization来解决,而不依赖多个源域。instance normalization只是对特征进行标准化,而没有考虑通道之间的相关性。然而,许多研究认为特征协方差包含领域特定的风格,如纹理和颜色。这意味着对网络应用实例归一化可能不足以实现域泛化,因为特征协方差没有被考虑。
- 白化变换是一种去除特征相关性并使每个特征具有单位方差的技术。已经证明该功能有效地消除了特定领域的样式信息,因此它可以提高泛化能力的特性表征,但尚未充分探讨DG。然而,单纯采用白化变换来提高dnn的鲁棒性并不简单,因为它可能同时消除了领域特定的风格和领域不变的内容。解耦这两个因素并有选择地去除特定于领域的风格是本文的主要研究范围。
贡献点
- 我们提出了一种用于域泛化的实例选择性白化损失算法,该算法从特征表示的高阶统计量中分离出域特异性和域不变特性,并有选择地抑制域特异性的特性。
- 我们所提出的loss可以很容易地应用于现有的模型中,在可以忽略计算代价的情况下显著提高了泛化能力。
- 我们将提出的损失应用于DG环境下的城市场景分割,并在定性和定量的方式上显示了我们的方法比现有方法的优越性。
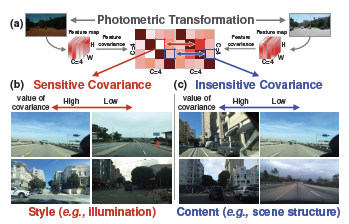
| Fig.1 (a)我们首先确定对光度变换敏感的特征协方差,并检查每组图像的趋势。(b)敏感协方差:光照(即样式)趋向于显著变化。(c)不敏感协方差:对场景结构差异(即内容)敏感,但不受光度变换的影响。因此,我们的目标是有选择地去除可能导致域移动的风格敏感的协方差 |
背景知识
特征相关性
特征相关性(即gram矩阵或协方差矩阵)获取图像的风格信息。此后,大量研究利用了风格转换、图像到图像转换、域适应和网络结构中的特征相关性。特别是白化变换,去除特征相关性,使每个特征具有单位方差,有助于从特征表示中去除风格信息。
白化变换(Whitening transformation, WT)
-
定义 白化变换是一种线性变换,它使每个通道的方差项等于1,并且使每对通道之间的协方差等于0,目的是去除数据中的冗余,使通道间不相关。 定义中间的feature map为 \(X\in R^{C\times HW}\), 白化变换的特征映射需满足:
\[\tilde{X} \cdot \tilde{X}^\top = (HW) \cdot \mathbf{I} \in R^{C\times C}\] \[\tilde{X} = \Sigma_{\mu}^{-\frac{1}{2}}(X-\mu \cdot \mathbf{1}^\top)\]\(\mathbf{1} \in R^{HW}\) 是一个1的列向量,\(\mu\) 和 \(\Sigma_{\mu}\) 分别是均值向量和协方差矩阵:
\[\mu = \frac{1}{HW}X \cdot \mathbf{1}^\top \in R^{C \times 1}\] \[\Sigma_{\mu} = \frac{1}{HW}(X-\mu \cdot \mathbf{1}^\top)(X-\mu \cdot \mathbf{1}^\top)^\top \in R^{C \times C}\]\(\Sigma_{\mu}\) 能够被特征分解为 \(\mathbf{Q} \Lambda \mathbf{Q}^\top\) 其中,\(\mathbf{Q}\in R^{C \times C}\) 是特征向量的正交矩阵,\(\Lambda \in R^{C \times C}\) 是对角矩阵包含特征向量对应的特征值,因此,可以计算 \(\Sigma_{\mu}^{-\frac{1}{2}}\) 协方差矩阵平方根的倒数:
\[\Sigma_{\mu}^{-\frac{1}{2}} = \mathbf{Q} \Lambda^{-\frac{1}{2}}\mathbf{Q}\] -
WT的局限性
我们可以计算白化变换矩阵 \(\Sigma_{\mu}^{-\frac{1}{2}}\) 但是特征值分解的计算是非常昂贵的,为了解决这个问题,提出了GDWCT深度白化变换,通过定义loss,隐式的使协方差矩阵 \(\Sigma_{\mu}\) 接近单位矩阵 \(\mathbf{I}\):
\[L_{DWT} = \mathbf{E}[\parallel \Sigma_{\mu} - \mathbf{I} \parallel _1]\]然而,对所有协方差元素进行白化可能会降低特征识别,并扭曲对象的边界,因为领域特定的风格和领域不变的内容同时被编码在特征映射的协方差中。
模型框架
Instance Whitening Loss
公式(6)可被分解为:
\[\parallel \Sigma_{\mu(i,i)} - \mathbf{I} \parallel _1 = \parallel \frac{x_i^\top \cdot x_i}{HW} - 1 \parallel _1 = \parallel \frac{\mid x_i \mid \mid x_i\mid cos0^{\circ}}{HW} - 1 \parallel _1\] \[\parallel \Sigma_{\mu(i,j)} \parallel _1 = \parallel \frac{x_i^\top \cdot x_j}{HW} - 1 \parallel _1 = \parallel \frac{\mid x_i \mid \mid x_j\mid cos0^{\circ}}{HW}\parallel _1\]其中 \(\Sigma_{\mu(i,i)}\) 是矩阵的对角元素, \(\Sigma_{\mu(i,j)}\) 是矩阵的非对角元素,\(x_i \in R^{HW}\) 定义为feature map X的第i个通道。
为了解决这个问题,首先将feature map进行实例标准化
\[X_s = (diag(\Sigma_{s}))^{-\frac{1}{2}} \odot (X-\mu \cdot \mathbf{1}^\top)\]标准化后的协方差矩阵可以计算:
\[\Sigma_{s} = \frac{1}{HW}(X_s)(X_s)^\top \in R^{C\times C}\]此时由于进行了标准化的操作,协方差矩阵对角线的元素已经被置为1,所以只需要将非对角线元素最小化到0来进行白化变换。因为协方差矩阵是对称的,所以loss只应用到上三角部分。
instance whitening (IW) loss可以定义为:
\[L_{IW}=\mathbf{E}[\parallel\Sigma_{s} \cdot \mathbf{M} \parallel _1]\]\(\mathbf{E}\) 表示算数平均值,\(\mathbf{M} \in R^{C\times C}\)为严格的上三角矩阵
\[M_{i,j}= \begin{cases} 0,\quad &if\quad i\ge j\\ 1,\quad &otherwise \end{cases}\]Margin-based relaxation of whitening loss
实例白化损失将所有协方差元素抑制为零,因此会对dnn中特征的鉴别能力产生不利影响。为了解决这个问题,提出了一种实例松弛白化(IRW)损失 ,以维持的鉴别能力所必需的协方差元素.IRW损失的设计使总协方差的期望值在指定的范围内,而不是接近于零,即:
\[L_{IRW} = max(\mathbf{E}[\parallel\Sigma_{s} \cdot \mathbf{M} \parallel _1] -\delta ,0)\]Separating Covariance Elements
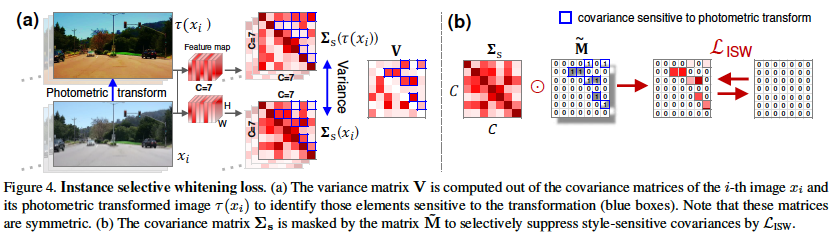
- 图4展示了ISW的训练流程,首先获取两个图像的feature map分别计算出协方差矩阵,然后计算两个协方差矩阵的方差矩阵 $$ V\in R^{C\times C}:
从第i个图像的两个协方差矩阵的每个元素的均值 \(\mu _{\Sigma _i}\) 和方差 \(\sigma_i^2\)
\[\mu_{\Sigma_i} = \frac{1}{2}(\Sigma_{s}(x_i)+\Sigma_{s}(\tau(x_i)))\] \[\sigma_{i}^2 = \frac{1}{2}(( \Sigma_{s}(x_i)-\mu_{\Sigma_i} )^2+( \Sigma_{s}(\tau(x_i))+\mu_{\Sigma_i} )^2)\]假设方差矩阵V表示相应的协方差对光度变换的敏感性。这意味着方差值高的协方差元素包含了领域特有的风格,如颜色和模糊度。为了识别这些元素,对严格上三角形元素应用k-means聚类,根据聚类可以分成两组,一组是方差值较高的(风格信息),另一组是方差值较低的(结构信息)。
最后,提出了一种选择性实例白化(ISW)损失,它选择性地只抑制到样式编码的协方差。
\[\tilde{M}_{i,j}= \begin{cases} 1,\quad &if\quad V_{i,j} \in G_{high}\\ 0,\quad &otherwise \end{cases}\]ISW loss被定义为:
\[L_{ISW}=\mathbf{E}[\parallel\Sigma_{s} \cdot \mathbf{\tilde{M}} \parallel _1]\]